Physics#2 Chapter1

Chapter 1 (Electric Charges and Fields)

Important Formulas and Notes

Laws of Electrostatics

i) Like charges repel and unlike charges attract

ii)There are only two kinds of charge positive and negative

Conventionally when a glass rod is rubbed against silk the glass rod attains positive and silks attain negative charge

It was Benjamin Franklin who gave the name positive and negative charge

An electroscope is an instrument used to detect the charges

We can charge a neutral body by rubbing

The charge can be transfered from one body to another neutral body by

i) Conduction (with actual contact of two)

ii) Induction (without actual contact of the two)

The body which looses electrons become positive and those which receives electron become negative

Basic properties of electric charge

• Additivity of charges (positive and negative charges can be added algebraically)
• Conservation of charges(charge can neither be created nor be destroyed)
• Quantisation of charge ( charges are integral multiples of e (charge of an electron=1.602192 × 10^-19 )ie Q=ne

Coulomb's Law

The law states that " the electrostatic force between two charges is directly proportonal to the product of their charges and inversely

proportional to the square of the distance between them"

This is an inverse square law just like Newton's law of Gravitational

ε₀=Permitivity of free space =8.854 × 10^-12 N^-1m^-2

            

In the above equation if q₁ and q₂ are like charges then F is taken as positive(repulsion) and if q₁ and q₂ are opposite signs

then F is negative ie attraction

Forces between multiple charges

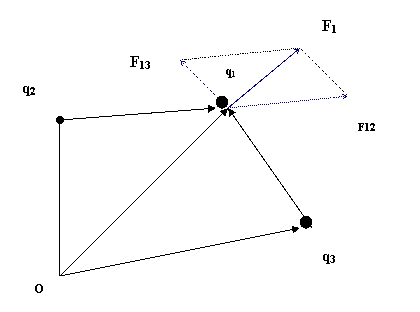
Let the distance between q₁ and q₂ be r₁₂ and between q₁ and q₃ be r₁₃

F₁₂ is the force on q₁ by q₂ and F₁₃ is the force exerted on q₁ by q₃So the resultant force F acting on q₁=F₁₂+ F₁₃

F is found by using parallelogram law of forces.(refer Physics Numericals)

This is applicable to many charges and the principle is called

the Principle of Superposition

Electric Field

It is defined as the force exerted on a unit positive charge by a source charge Q placed at that point

ie if a charge Q placed at a ponit exert a force on unit positive charge when placed around its viscinity (here at a distance of r apart) ie

. ^. . F(r)=q E(r)The field exists at every point in three dimensional space

• For positive charge the field will be directed outwards (as shown below)
• For a negative charge the field will be directed inwards
• At equal distance around a point charge the field will be the same (ie field has a spherical symmetry)
• 
  

Electric Field due to a system of Charges

Let us asuume that there are n charges q₁,q₂,..........q_n are arranged and we have to find the resultant field (E(r)) at the point P
here also we are applying the Principle of superposition

E(r)=E₁(r) + E₂(r)+...........E_n(r)
ie E(r)=∑_i=1ⁿ E_i(r)

The physical significance of electric field is that the accelarated motion of one charge produces electromagnetic waves, which

then propagate with a speed c and reach the second charge and causes a force on this charge

Electric field lines

These lines are vector representation of electric field the length of these lines is proprtional to the field strength and direction

of this vector gives the direction of the field

The strength of electric field has a (1/r²) dependence

We can also infer the strength of field from its degree of crowdness ie number of lines passing through a given area

eg: If 10 lines are passing through an area of 1units and 100 lines are passing through 50 units then the field strength

is more in first case because in first case number of lines passing per unit area is 10 and in the second case it is only 2

Some general properties of Field Lines

• Field lines starts from positive charge and end at negative charge. If there is a single charge, they may start or end at infinity
• In a charge free region the electric field lines are continuous without any break
• The field lines never cross each other (since the tangent at the point of field lines is the direction of field; at a point two tangents in not possible)
• Electrostatic field lines do not form any closed loops( conservation of charge )

Electric Flux

The measure of number of lines passing per unit area placed normal to the field at a point is called the Electric Flux (Φ)

It is a scalar quantity

E. ∆S = E ∆S cosθ =∆Φ

Where E is the field and ∆S the surface area through which the field lines passes and θ is the angle between E and the outward normal to ∆S

(Note that angle of a plane with any other reference is the angleof the normal to the plane with reference )

Φ=∑E. ∆S (or it can be obtained by integrating ∆Φ)

(refer Physics Numericals)

Electric Dipole

It is a pair of equal and opposite charges seperated by a distance

ie point charges +q and -q seperated by a distance 2a and the direction of diploe is taken from -q to +q (as in figure)

The dipole moment p=One of the charge × distance between them=q ×2a =2qa

The field of an electric dipole

It can be found out by coulomb's law and principle of superposition of field by +q and -q charges

But the simple cases are i) field along the axis of the dipole ii) along the equitorial plane ie an axis perpendicular the dipole axis through the centre

 

i) Field along the axis of the dipole ( at point P which is r apart from centre of the dipole axis)

ii)Field along the point ( point P which is r apart from centre of the dipole axis) which is on equitorial plane of the dipole

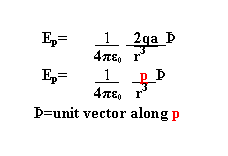
From the above equation it is clear that the field along the axial line is twice that of field along the equtorial plane

The above two equations are formed by considering r>>a

The direction of Resultant field (E_p) in the case of equitorial plane is opposite to the direction of diploe (p)

The point dipole is a dipole where q is a point charge ie q approaches infinity and 2a approaches zero so the product never vanishes

The dipole moment have significane in ionic compounds and this gives rise to many chemical and physical properties to this class of compounds

Dipole in a Uniform Field

If a diploe is placed along a uniform field (E) a couple or torque(τ) will be formed and it rotates the diploe

Magnitude of torque= 2qa Esinθ

τ=p × E

The torque will tend to allign the diploe along the direction of field E when it is alligned with E ie (θ=0) torque is zero

The two forces acting on the diploe are +qE and -qE ie the force depends on the orientation of E

Continuous Charge Distribution

Surface Charge density (σ) = ∆Q/ ∆S (SI unit is Cm^-2)

Linear Charge density (λ)= ∆Q / ∆l (SI unit is Cm^-1)

Volume Charge density (ρ)= ∆Q / ∆V (SI unit is Cm^-3)

Gauss's Law

A point charge has spherical symmetry Let ∆S be a small elemental area on the surface of this sphere of radius r formed by a charge q as shown below

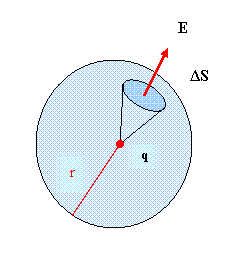
Let ∆φ be the flux through the small elemental area ∆S

∆φ= E.∆S=K / r² .∆S (where K = 1_ )

                                                    4πε₀

. ^. .Φ= ∑ K/ r² .∆S=K/ r²∑ ∆S

. ^. .Φ=K/ r²× 4πr²

_1_   (1/ r² ) × 4πr²

4πε₀       

 . ^. .Φ=q/ε₀ =E.S 

Thus we state Gauss theorem as the electric flux through a closed Gaussian surface is 1/ε₀   times q

The important points regarding Gauss theorems are

• Gauss law is applicable to any closed surface irrespective of its shape or size
• q in the equation involves sum of all charges enclosed by the surface, the charge may be located anywhere inside the surface
• there may be charge outside the Gaussian surface it is not considerd only inside the surface is considering
• Gauss law varifies Coulomb's Law

(refer1.18) Physics Numericals

Gauss Law can be used to find the field due to an infinitely long straight wire

Consider an infinitely long straight wire of linear charge density λ and we have to find a field at P at a distance of r from its axis. The wire has a cylindrical symmetry

and the wire is positively charged as shown in figure

The flux through the top and bottom circular surface cancell each other but the curved surface area imparts a flux at point P

as per Gauss Law, Flux ( Φ)=E×Curved surface area of cylinder= E×2πrl=q/ε₀ . ^. .E=(½πε₀)(q/rl)= (½πε₀) ( λ/r) (since q=λl)

Field due to a uniformly charged Infinite plate

Let σ be the uniform charge density of the plate and the x axis is normal to the surface of the plane and by the symmetry the field along the y axis and z axis

are not under consideration

The unit vector normal to one of the side face is along -x axis and the opposite face is along + x axis so the flux, E.∆S through the both surface add up

So the net flux through the Gaussian surface is 2EA (where A is the area of the plate)

 . ^. .2EA= ( σA)/ε₀

or E= σ/2ε₀

In vector form E=( σ/2ε₀) ň (refer 1.19) Physics Numericals
Field due to a uniformly charged spherical shell
Let σ be the surface charge density of a shell of radius R by the symmetry the Gaussian surface as marked has a spherical symmetry

The field at a Point P which is r distance apart from the centre of the shell then there exist two conditions

i) the Gaussian surface outside the shell (r>R)-as shown in the figure

ii) the Gaussian surface lying inside the shell( r<R)

Field outside the shell (r>R)

By Gauss theorem ES=q/ ε₀=σA/ ε₀(q=σA)

ie E×4πr²= σ×4πR²/ε₀ ( Surface area of shell,A=4πR² and area of Gaussian surface, S= 4πr²)

E=σR² /ε₀r²

or

E×4πr²=q/ ε₀

 . ^. .E= _1_   (q / r² ) ř...............................(1)

           4πε₀

Thus for points outside the shell, the field due to a uniformly charged shell is as if the entire charge of the shell is concentrated at its centre

ie the equation (1) is similar to field due to a point charge q at r distance E(r)

Field inside the shell (r<R)

In this case the Gaussian surface under consideration is inside the shell (point P inside the shell) so r<R

Here the flux through the Gaussian sufrace as before= E×4πr²

but the charge is only on the surface of the shell or supposed to concentrate at the centre

 . ^. . q=0 at point P

 . ^. . E×4πr²=0

=>E=0

Thus the field due to uniformly charged shell is zero at all points inside the shell

^{****End of chapter 1*****}