Quantum Mechanics

`\color{green}"The following steps explain How to handle a complex power"`

`x^{a+ib}=x^{a}.x^{ib}=x^{a}.(e^{log(x)})^{ib}because x=e^{log(x)}`

`=x^a.e^{ib.log(x)}=x^{a}[cos(b.log(x))+isin(b.log(x))]`  (by de Moivres theorem)

In the above result put a=0 and b=1 results in

`x^i=[cos(log(x))+isin(log(x))]`

(1)

(2)


(3)

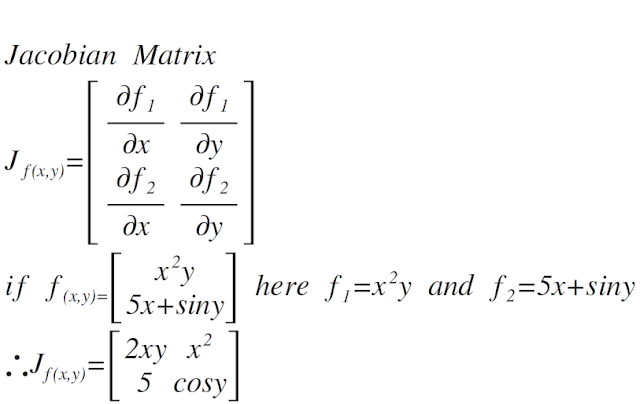
Comments

Post a Comment

Popular posts from this blog

Hyperbolic Paraboloid

Image
Graphs and Level curves of functions of Two variables Definitions The set of points (x,y) in the plane where a function f (x,y) has a constant value f(x,y)=c is called a level curve of f The set of all points (x,y,f (x,y)) in space, for (x,y) in the domain of f, is called the graph of f The graph of f is called the surface z=f (x,y) The equation of the following hyperbolic paraboloid is `z=50+x^2-y^2`
Read more

Renewable Energy-Solar

The conventional energy sources are depleting at an exponential  rate .The energy crisis is a major concern for the nation around. The coal will last long only for 100 years or less petroleum resource will be exhausted nearly in 50 years time. The oil producing countries it self is moving towards the introduction of renewable energy sources , major among them is Solar energy. The energy production in the sun is  by the  nuclear fusion , hydrogen in the core of sun is converting in to heavier nucleus helium during this process the nuclear binding energy is liberating in the form useful energy . The plants can absorb the visible light and utilize it  for photosynthesis . The use of solar energy by natural means is coming only 1 to 2 % , rest of the energy is un utilized The solar energy capturing technique (Photo Voltaic) was introduced by Charles Fritts   in the year 1883 The solar energy can be  utilized in the following ways 1.  ...
Read more